抛物线的顶点坐标公式是:(-b/2a,(4ac-b²)/4a)。这个公式的推导过程如下:一般的二次函数表达式为y=ax²+bx+c(a≠0)。由公式a×x²+(b×x)+c=0,配方后可得到(x+b/2a)²=(b²-4ac)/4a。根据任何数的平方都是非负数,可知当x=0时,(x+b/2a)²=(b²-4ac)/4a有最小值,那么它的顶点就是y的最小值或最大值。此时,x=-b/2a,y=(4ac-b²)/4a。所以,抛物线的顶点坐标是(-b/2a,(4ac-b²)/4a)。
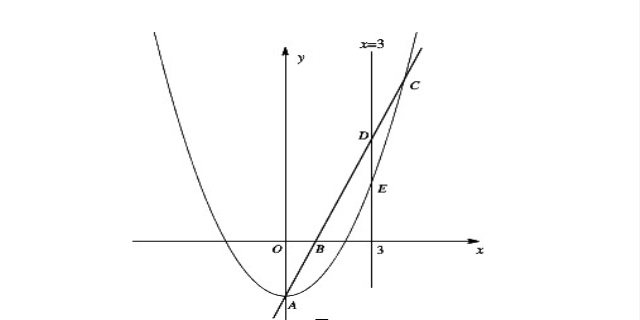
抛物线顶点坐标公式
这个公式在求解抛物线的顶点坐标时十分方便,因为它不需要解方程就能直接得出结果。这个公式不仅适用于求解一般的二次函数的顶点坐标,还适用于其他形式的抛物线。此外,如果抛物线开口向上,那么顶点就是最低点;如果抛物线开口向下,那么顶点就是最高点。这个结论也进一步体现了抛物线顶点坐标公式的实用性。